题目翻译
你现在拥有 $n$ 架飞机,每架飞机有一个出发点 $(x_i,y_i)$,每架飞机每秒向指定方向飞 $0.1$ 个单位,问什么时候会发生第一次撞击(撞击指两架飞机坐标完全相同),不会发生输出 SAFE。
方向:
- $\tt U$ 向上,即向 $y$ 轴正方向运动。
- $\tt R$ 向右,即向 $x$ 轴正方向运动。
- $\tt D$ 向下,即向 $y$ 轴负方向运动。
- $\tt L$ 向左,即向 $x$ 轴负方向运动。
$1\leq n\leq 2\times 10^5,0\leq x_i,y_i\leq 2\times 10^5$。
前言
空心黄,五分钟胡完正解实现了一个多小时,终究还是太菜了。
题目思路
什么初二一次函数入门题。
首先,飞机相遇有两种大情况,共线面对面或者垂直。
面对面还贡献很好处理,我们把每个方向的飞机按 $x$ 储存在 $4\times 2\cdot10^5$ 个 vector 里,枚举 $x$ 找一下即可。
垂直就要分 $4$ 个小情况了,这里介绍 $2$ 个情况,剩下两个是一模一样只是换个方向。
但是不要吝啬草稿纸,笔者就是因为发现了 $2$ 种情况非常高兴,剩下 $2$ 种分类错了调试了一个小时。
我们现在的问题是,如何知道了一个点,找到别的它垂直的点?
一个小类情况是 UL 和 RD 两种相遇,以 UL 为例,应该长这样。
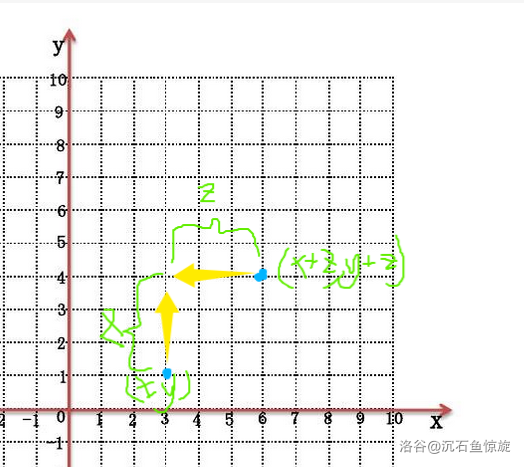
不难发现,我们知道了一个 $(x,y)$,能很容易发现所有的 $(x+z,y+z)$ 能和它垂直。再分析一下,$y-x=(y+z)-(x+z)$,也就是他们的横纵坐标差 $z$ 是相同的。那么我们按 $z$ 开若干 vector 记录即可。实现要注意方向和负数下标。
另一小类是 RU 和 DL。这里以 DL 为例,应该长这样。
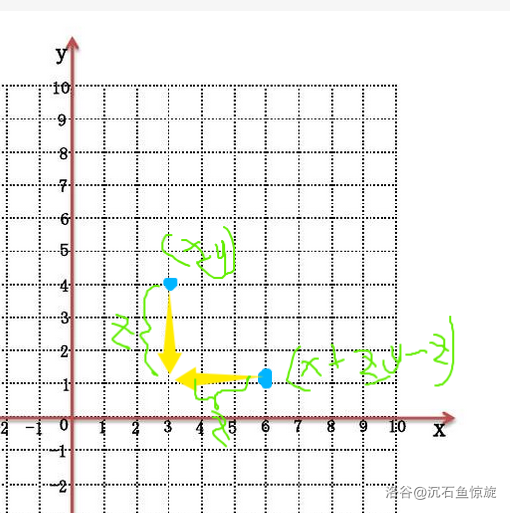
同样不难发现,我们知道了一个 $(x,y)$,能很容易发现所有的 $(x+z,y-z)$ 能和它垂直。再分析一下,$x+y=(x+z)+(y-z)$,也就是他们的横纵坐标之和是相同的。那么我们按横纵坐标之和开若干 vector 记录即可。实现要注意方向。
我们找点可以双指针跑来优化。因为需要排序,所以时间复杂度 $\mathcal O(n\log n)$,空间复杂度 $\mathcal O(n)$。
虽然看上去思维难度不高,但写得拉一点还是很恶心的。
