蒸馍身边一群大神不会普通莫队。

现在每天半夜不写点根号算法都睡不着。根号算法个个是优雅的算法/se

莫队

处理离线区间询问。

名字由来是因为是莫涛整理的。

普通莫队

简介

可以较优复杂度从 $[l\pm1,r\pm1]$ 转到 $[l,r]$。

当 $n,q$ 同阶时，若转移为 $\mathcal O(1)$，总复杂度即为 $\mathcal O(n\sqrt n)$。同理，转移为 $\mathcal O(log n)$ 复杂度即为 $\mathcal O(n\sqrt n\log n)$。

$n,q$ 不同阶参考 OI Wiki 的复杂度分析。

https://oi-wiki.org/misc/mo-algo/#%E5%A4%8D%E6%9D%82%E5%BA%A6%E5%88%86%E6%9E%90

排序

对于询问的排序，一般是对 $L$ 分块，先按块排序，每个块内再按 $R$ 排序。一般这样即可，但是更好的写法可以继续奇偶性优化少掉不同块内 $R$ 从 $n$ 再次回到 $1$ 的过程。

以下为排序代码，其中 $fa_i$ 表示 $i$ 在那一块。

bool cmp(node a, node b)
{
    if (fa[a.L] != fa[b.L])
        return a.L < b.L;
    if (fa[a.L] & 1)
        return a.R > b.R;
    return a.R < b.R;
}

也就是说，不进行奇偶性优化的莫队，询问排序后长这样：

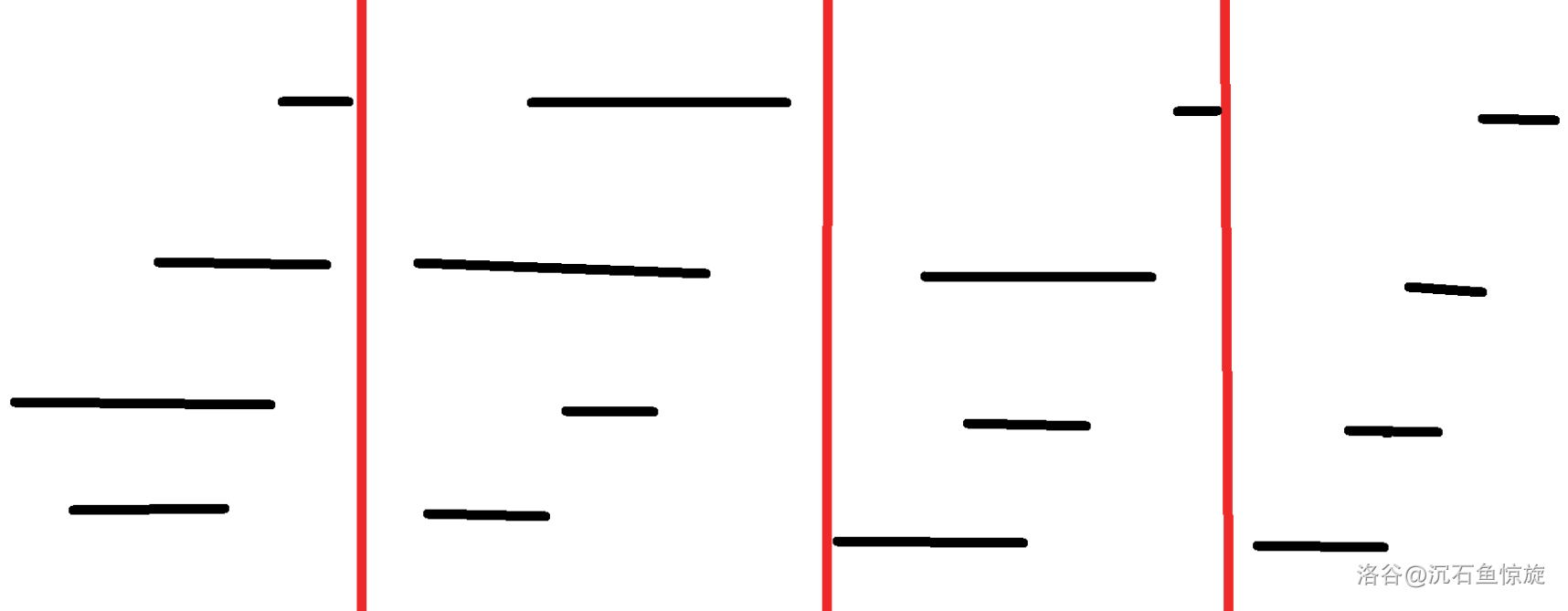
而进行了奇偶性优化的话：

这样子就可以让 $R$ 更加连贯。

图中红线表示分块的界线，黑线表示区间询问范围。

实现

int L = 1, R = 0;
for (int i = 1; i <= q; i++)
{
    while (L > Query[i].L)
        add(--L);
    while (R < Query[i].R)
        add(++R);
    while (L < Query[i].L)
        del(L++);
    while (R > Query[i].R)
        del(R--);
    ans[Query[i].id] = ANS;
}

其中 $add(x)$ 和 $del(x)$ 分别表示添加第 $x$ 个位置和删除第 $x$ 个位置进行的操作。

当然，有的题 $L$ 和 $R$ 的添加删除是不一样的。

这是个循环位置的顺序，参考 https://oi-wiki.org/misc/mo-algo/#%E8%BF%87%E7%A8%8B 关于四个循环位置的讨论。一般来说你只要保证先扩张后缩减是不会有问题的。

例题

P1972 [SDOI2009] HH的项链

我们将此题作为莫队模板进行讲解。

可是这题莫队标签都没有！那是因为大家不会卡常。

记录颜色数，即为记录 $h_i$ 表示 $i$ 在序列中出现的次数，新出现加一种颜色，被删完少一种颜色。

那么我们很快就能码好：

#include <bits/stdc++.h>
using namespace std;
int fa[1000020];
int a[1000020];
int ans[1000020];
int h[1000020];
int n, len, ANS, q;
#define getchar() p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++
char buf[1000000], *p1 = buf, *p2 = buf;
inline int read()
{
    register char c = getchar();
    register int x = 0;
    while (c < '0' || c > '9')
        c = getchar();
    while (c >= '0' && c <= '9')
        x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return x;
}
struct node
{
    int L, R, id;
} Query[1000020];
bool cmp(node a, node b)
{
    if (fa[a.L] != fa[b.L])
        return a.L < b.L;
    if (fa[a.L] & 1)
        return a.R > b.R;
    return a.R < b.R;
}
int main()
{
    n = read();
    len = sqrt(n);
    for (int i = 1; i <= n; i++)
    {
        a[i] = read();
        fa[i] = (i + len - 1) / len;
    }
    q = read();
    for (int i = 1; i <= q; i++)
    {
        int L, R;
        L = read();
        R = read();
        Query[i] = {L, R, i};
    }
    sort(Query + 1, Query + q + 1, cmp);
    int L = 1, R = 0;
    for (int i = 1; i <= q; i++)
    {
        while (L > Query[i].L)
            ANS += (++h[a[--L]] == 1);
        while (R < Query[i].R)
            ANS += (++h[a[++R]] == 1);
        while (L < Query[i].L)
            ANS -= (--h[a[L++]] == 0);
        while (R > Query[i].R)
            ANS -= (--h[a[R--]] == 0);
        ans[Query[i].id] = ANS;
    }
    for (int i = 1; i <= q; i++)
    {
        printf("%d\n", ans[i]);
    }
    return 0;
}

诶，T 了！本题莫队真的过不去吗？

我的评价是我这题不关同步的 cin 都过了。

#include <bits/stdc++.h>
using namespace std;
int fa[1000020];
int a[1000020];
int ans[1000020];
int pre[1000020];
int nxt[1000020];
int p[1000020];
int n, len, ANS, q;
#define getchar() p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++
char buf[1000000], *p1 = buf, *p2 = buf;
inline int read()
{
    register char c = getchar();
    register int x = 0;
    while (c < '0' || c > '9')
        c = getchar();
    while (c >= '0' && c <= '9')
        x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return x;
}
struct node
{
    int L, R, id;
} Query[1000020];
bool cmp(node a, node b)
{
    if (fa[a.L] != fa[b.L])
        return a.L < b.L;
    if (fa[a.L] & 1)
        return a.R > b.R;
    return a.R < b.R;
}
int main()
{
    n = read();
    len = sqrt(n);
    for (int i = 1; i <= n; i++)
    {
        a[i] = read();
        fa[i] = (i + len - 1) / len;
        nxt[i] = n + 1;
        pre[i] = p[a[i]];
        nxt[pre[i]] = i;
        p[a[i]] = i;
    }
    q = read();
    for (int i = 1; i <= q; i++)
    {
        int L, R;
        L = read();
        R = read();
        Query[i] = {L, R, i};
    }
    sort(Query + 1, Query + q + 1, cmp);
    int L = 1, R = 0;
    for (int i = 1; i <= q; i++)
    {
        while (L > Query[i].L)
            ANS += (nxt[--L] > R);
        while (R < Query[i].R)
            ANS += (pre[++R] < L);
        while (L < Query[i].L)
            ANS -= (nxt[L++] > R);
        while (R > Query[i].R)
            ANS -= (pre[R--] < L);
        ans[Query[i].id] = ANS;
    }
    for (int i = 1; i <= q; i++)
    {
        printf("%d\n", ans[i]);
    }
    return 0;
}

为什么这样可过呢，我们发现，观察一个数在序列中是否是只出现一次，只需要看同一颜色的数，是否已经出现过了。有点废话文学，但是『只需要看同一颜色的数，是否已经出现过了』就是记录这个数上一次出现的位置和下一次出现的位置。

所以，我们考虑记录 $pre_i$ 和 $nxt_i$ 表示 $a_i$ 上一次或下一次出现的位置用来辅助区间转移。

这样子就可以做到莫队过程访址连续，真正的 $\mathcal O(n\sqrt n)$。

P1494 [国家集训队] 小 Z 的袜子

记录每个区间此时颜色数量，那么颜色数量 $-1$ 即为此时这个颜色能配成多少对。答案分母显然是 $\dbinom{R-L+1}{2}$。分子即为所有颜色能配成多少对。

P2709 小 B 的询问

也是区间数颜色。每种颜色个数平方一下即可。

P3901 数列找不同

判断区间颜色数是否 $=R-L+1$。

CF351D Jeff and Removing Periods

为了方便描述，我们约定数值相同的数为同一颜色的数。

有 $n$ 个数，我们定义一次操作为：选择若干个同颜色数，使得他们在序列中的位置为一个等差数列。删除它们。

操作完之后可以重排整个序列。

有 $q$ 个询问，每次询问给定 $[l,r]$，求至少几次操作能全部删除 $[l,r]$。

询问互不影响。

$1\leq n,q,a_i\leq 10^5$

http://blog.cyx2009.top/archives/250/ 查看。

CF351D Jeff and Removing Periods 题解

闲话和等差数列过不去了。碰上等差数列就要调 1h。题目翻译为了方便描述，我们约定数值相同的数为同一颜色的数。有 $...

或洛谷题解区最高赞题解。

ABC293G Triple Index

给定长度为 $N$ 的数列 $a_1,a_2,\cdots,a_N$。

$q$ 组询问，每组询问给定 $l,r$ 且 $1\le l\le r \le n$，问存在多少个三元组 $(i,j,k)$，使得 $l\le i < j<k\le r$ 且 $a_i=a_j=a_k$。

考虑增加颜色和删除颜色贡献，设当前位置的颜色是 $x$，共显示 $\pm \dfrac{(h_x-1)(h_x-2)}{2}$。其中 $h_i$ 表示颜色 $i$ 的个数。

TENKA1_2014_FINAL D

$m$ 组询问，每次给定 $n,k$，求 $\sum\limits_{i=0}^k \binom{n}{i}$。

$1 \le n, m, k \le 10^5$。

很好数学，爱来自莫队。

$\dbinom{n}{k-1}\to\dbinom{n}{k},ans\gets ans+\dbinom{n}{k}$

$\dbinom{n}{k+1}\to\dbinom{n}{k},ans\gets ans-\dbinom{n}{k+1}$

$\dbinom{n-1}{k}\to\dbinom{n}{k},ans\gets 2ans-\dbinom{n-1}{k}$

$\dbinom{n+1}{k}\to\dbinom{n}{k},ans\gets \dfrac{ans+\dbinom{n}{k}}{2}$

改变 $k$ 是显然的，改变 $n$ 用帕斯卡法则拆一下即可得到 $\dbinom{n-1}{k}\to\dbinom{n}{k}$ 的答案变化，另一个同理。

SP DQUERY - D-query

给出一个长度为 $n$ 的数列，$a_1,a_2,\dots,a_n$ ，有 $q$ 个询问，每个询问给出数对$(i,j)$，需要你给出 $a_{i},a_{i+1},\dots ,a_{j}$ 这一段中有多少不同的数字。

也是区间数颜色。

最后修改：2024 年 02 月 02 日
© 允许规范转载
v我50吃疯狂星期四