题目思路
原来这种多边形转成笛卡尔树建树是常见 trick。练的太少导致的。
但是这题其实不用笛卡尔树建树,因为 DP 部分复杂度较高其实这个优化(至少在我的程序上)没有太大作用。
为了方便描述,定义中国象棋中的『車』为题目中的颜色,本质一样。
考虑把这个多边形转成树,分割方式就是以底层开割。
机房电脑的 NOI Linux 2.0 没有好用的画图软件,这里用一张别人题解的图。
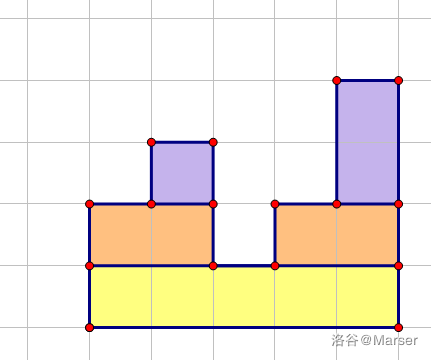
我们找到最低点,分成左右两边,分治建树。把最低端想象成子树的根,向上的一层不同颜色既是子节点。
如果不能分成恰好两棵子树,其实没有影响,把某两个放到一起先当成一个节点下一次分开来就好了,没有必要特别判这个问题。
然后这个问题被我们抽象成了树上问题,直接采取树形 DP 解决。
这里再提一个东西:
大小为 $n\times m$ 的棋盘,放入 $k$ 个不同的『車』,互不攻击的方案数是 $\binom{n}{k}\times \binom{m}{k}\times k!$。
考虑选择 $k$ 行再选择 $k$ 列,方案数是 $\binom{n}{k}\times \binom{m}{k}$。因为『車』不同,乘上全排列方案数 $k!$。
回归本题,设计 $F_{u,i}$ 表示以 $u$ 为根的子树,放了 $i$ 个『車』的方案数。
但是直接乱转移复杂度有点烂,所以先处理 $G_{u,i}$ 表示以 $u$ 为根的子树,不包括矩形 $u$,也就是只考虑以 $u$ 的子节点为根的子树,放了 $i$ 个『車』的方案数。
$G$ 数组的转移是显然的,枚举两边分别放了几个。
以下定义 $ls$ 和 $rs$ 表示 $u$ 的左右子树根节点编号。
$$
G_{u,i}\gets \sum\limits_{j=0}^{i} F_{ls,j} \times F_{rs,i-j},\forall i\in[1,k]
$$
有了这个 $G$ 我们的 $F$ 就可以很快乐的转移了。枚举不包括自己的子树部分,放了几个,然后乘上自己选择的方案数。
但是,因为矩形之间联通,你需要处理有几列被子树部分的『車』覆盖的情况。直接把这几个位置扔掉就行了,剩下的同上面所说的方案数。
因此,$F$ 的转移呼之欲出。定义 $H_u,W_u$ 表示矩形 $u$ 的高和宽。
$$
F_{u,i}\gets \sum\limits_{j=0}^{i} \binom {H_u}{i-j}\times \binom {W_u-j}{i-j}\times G_{u,j},\forall i\in[1,k]
$$
总复杂度为 $\mathcal O(nk^2+n^2)$。
部分代码
const int N = 1e6;
Z fac[N + 20];
Z inv[N + 20];
Z C(int n, int i) { return n < 0 || i < 0 || n < i ? 0 : fac[n] * inv[i] * inv[n - i]; }
#define ls c[u][0]
#define rs c[u][1]
int n, k;
int h[520];
int H[520];
int W[520];
int c[520][2];
Z f[520][520];
Z g[520][520];
int rt;
int build(int l, int r)
{
if (l > r)
return 0;
int u = min_element(h + l, h + r + 1) - h;
ls = build(l, u - 1);
rs = build(u + 1, r);
H[ls] = h[ls] - h[u];
H[rs] = h[rs] - h[u];
W[u] = r - l + 1;
return u;
}
void dfs(int u)
{
f[u][0] = g[u][0] = 1;
if (!u)
return;
dfs(ls), dfs(rs);
for (int i = 1; i <= k; i++)
for (int j = 0; j <= i; j++)
g[u][i] += f[ls][j] * f[rs][i - j];
for (int i = 1; i <= k; i++)
for (int j = 0; j <= i; j++)
f[u][i] += C(H[u], i - j) * C(W[u] - j, i - j) * fac[i - j] * g[u][j];
}
int main()
{
fac[0] = 1;
for (int i = 1; i <= N; i++)
fac[i] = fac[i - 1] * i;
inv[N] = fac[N].pow(PPP - 2);
for (int i = N; i >= 1; i--)
inv[i - 1] = inv[i] * i;
read(n, k);
for (int i = 1; i <= n; i++)
read(h[i]);
rt = build(1, n);
H[rt] = h[rt];
dfs(rt);
cout << f[rt][k] << endl;
return 0;
}