题目翻译

平面直角坐标系中，有 $n$ 个木乃伊，分别为 $(x_i,y_i)$。你在原点 $(0,0)$ 上。

每一个时刻你可以往 $8$ 个相邻位置逃跑，或者待在原地。之后，木乃伊会向 $8$ 个方向移动到最靠近你（距离为欧几里得距离）的位置。多只木乃伊可以在一个格子。

问你多久可以不被木乃伊抓住。当然，也可能有永远不被抓住。

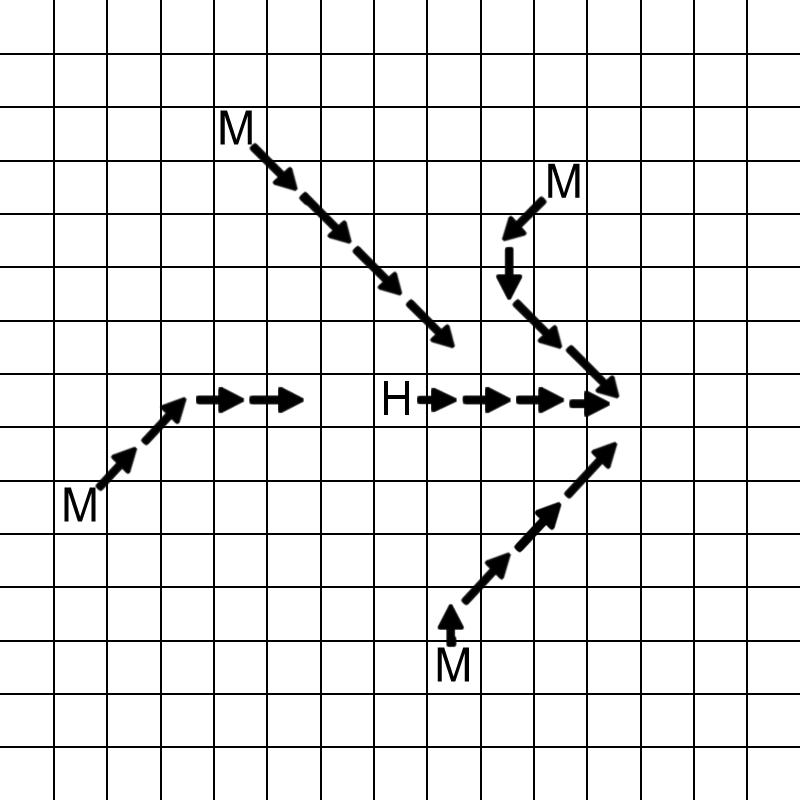
放一张样例的最佳走法的图：

原图来自于原版题面。其中，$\tt H$ 表示你，$\tt M$ 表示木乃伊。

题目思路

首先，二分答案是显然的。假设你现在没被抓住，且之前被抓住了，那么木乃伊一定是可以跟着你走让你现在也被抓住。因此，若你在 $k$ 时刻没被抓住，$k-1$ 时刻肯定也没被抓住。因此具有单调性。

然后考虑如何 check。我们发现因为是八方向，所以你得到的人和木乃伊的行走范围一定是一个正方形。

考虑你在 $k$ 时刻，不能走的位置，也就是木乃伊的行走范围。

那么只需要看一下，在你能行走的范围内，木乃伊的行走范围，占了多大。如果你的行走范围，木乃伊全都可以到达，就说明你会被抓住。

因此就是矩形面积并。注意多测清空。

完整代码

#include <bits/stdc++.h>
using namespace std;
#define getchar() p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++
char buf[1000000], *p1 = buf, *p2 = buf;
template <typename T>
void read(T &x)
{
    x = 0;
    int f = 1;
    char c = getchar();
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-')
            f = -f;
    for (; c >= '0' && c <= '9'; c = getchar())
        x = x * 10 + c - '0';
    x *= f;
}
template <typename T, typename... Args>
void read(T &x, Args &...y)
{
    read(x);
    read(y...);
}
typedef long long ll;
int n;
struct Seg
{
    int x, yd, yu, c;
};
vector<Seg> a;
vector<int> v;
struct SegTree
{
    struct node
    {
        int len, lzy;
    } t[200020 << 2];
#define ls id << 1
#define rs id << 1 | 1
    void push_up(int id, int l, int r) { t[id].len = (t[id].lzy ? v[r] - v[l - 1] : (l == r ? 0 : t[ls].len + t[rs].len)); }
    void build(int id = 1, int l = 1, int r = v.size() - 1)
    {
        t[id].len = t[id].lzy = 0;
        if (l == r)
            return;
        int mid = l + r >> 1;
        build(ls, l, mid);
        build(rs, mid + 1, r);
    }
    void add(int ql, int qr, int k, int id = 1, int l = 1, int r = v.size() - 1)
    {
        if (r < ql || l > qr)
            return;
        if (ql <= l && r <= qr)
            return t[id].lzy += k, push_up(id, l, r);
        int mid = l + r >> 1;
        add(ql, qr, k, ls, l, mid);
        add(ql, qr, k, rs, mid + 1, r);
        push_up(id, l, r);
    }
} T;
int Q(int x) { return lower_bound(v.begin(), v.end(), x) - v.begin() + 1; }
void add(int xl, int yd, int xr, int yu)
{
    if (xl > xr || yd > yu)
        return;
    v.push_back(yd), v.push_back(yu);
    a.push_back({xl, yd, yu, 1});
    a.push_back({xr, yd, yu, -1});
}
struct Mummy
{
    int x, y;
} mummy[100020];
bool check(int k)
{
    if (!n)
        return 0;
    v.clear(), a.clear();
    for (int i = 1; i <= n; i++)
    {
        int x = mummy[i].x, y = mummy[i].y;
        add(max(-k, x - k), max(-k, y - k), min(k + 1, x + k + 1), min(k + 1, y + k + 1));
    }
    sort(v.begin(), v.end());
    v.erase(unique(v.begin(), v.end()), v.end());
    sort(a.begin(), a.end(), [&](Seg a, Seg b)
         { return a.x ^ b.x ? a.x < b.x : a.c > b.c; });
    T.build();
    ll ans = 0;
    for (int i = 0; i + 1 < a.size(); i++)
    {
        int x = a[i].x, yd = a[i].yd, yu = a[i].yu, c = a[i].c;
        T.add(Q(yd), Q(yu) - 1, c);
        ans += 1LL * T.t[1].len * (a[i + 1].x - x);
    }
    return ans == 1LL * (k + k + 1) * (k + k + 1);
}
int testcase;
const int inf = 1e6;
int main()
{
    testcase++;
    read(n);
    if (!(~n))
        return 0;
    for (int i = 1; i <= n; i++)
        read(mummy[i].x, mummy[i].y);
    int L = 1, R = inf, ans = -1;
    while (L <= R)
    {
        int mid = L + R >> 1;
        if (check(mid))
            R = (ans = mid) - 1;
        else
            L = mid + 1;
    }
    if (~ans)
        cout << "Case " << testcase << ": " << ans << '\n';
    else
        cout << "Case " << testcase << ": never\n";
    main();
    return 0;
}