题目翻译

有一个矩形，四个顶点分别是 $x_1,y_1,x_2,y_2$。问在中间铺设正六边形，每个六边形不能整个超出矩形范围，可以最多超过 $\frac{3}{4}$，问最多能铺多少个。

如样例中，左下角的正六边形露出了 $\frac{3}{4}$，最下面第二个正六边形露出了 $\frac{1}{2}$。

题目思路

我们通过观察下图，很容易发现，这些正六边形摆放都是按以下规律：

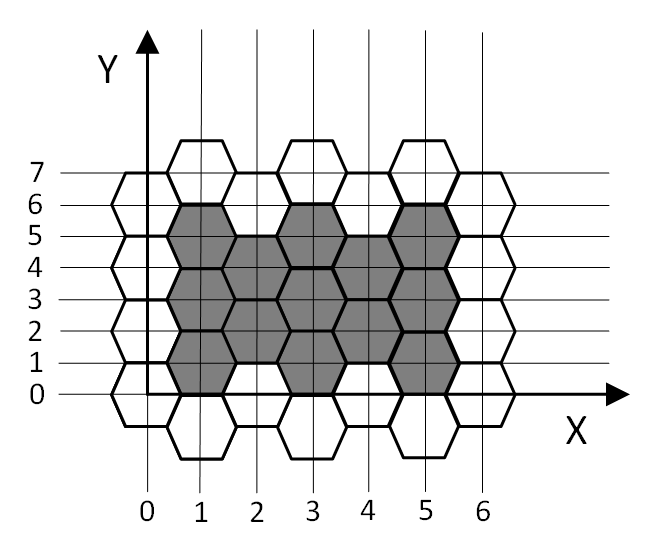
第奇数列，摆 $n$ 个。

第偶数列，摆 $n-1$ 个。

那么我们算出摆了多少列和 $n$ 具体是多少即可。

我们考虑把这张图，整体往左移半格。那么这张图的 $x_1=0.5$，$x_2=4.5$。再加上超过的部分，长就是 $4.5-0.5+1=5$。

同理，这张图的宽也加上超过的部分，就是 $5-1+2=6$。

那么通过长，算出奇列数和偶列数，通过宽，算出每列上面有多少的格子。

最后只要奇数列个数 $\times$ 奇数列的格子 $+$ 偶数列个数 $\times$ 偶数列的格子。

AC 代码

void solve()//记得开longlong
{
    ll x1,y1,x2,y2;
    cin>>x1>>y1>>x2>>y2;
    ll x=x2-x1+1,y=y2-y1+1;//算出长宽
    ll ans=((y+1)/2)*((x+1)/2)+((y-1)/2)*((x-1)/2);//结论带入
    cout<<ans<<endl;
}