前言

CSP-J 模拟赛教练放的一道原题，赛时 AC 了听同学说洛谷有，回来写题解。

题目思路

如何找到正方形的四个顶点

最简单的最容易思考到的方法：$\mathcal O(n^4)$ 或 $\mathcal O(n^3)$ 枚举四个顶点。

但由于 $n\leq3000$，肯定超时，复杂度肯定要控制在 $\mathcal O(n^2)$ 左右。

$\mathcal O(n^2)$ 意味着枚举两个点，我们来观察一下这两个点与另外两个点的位置关系。

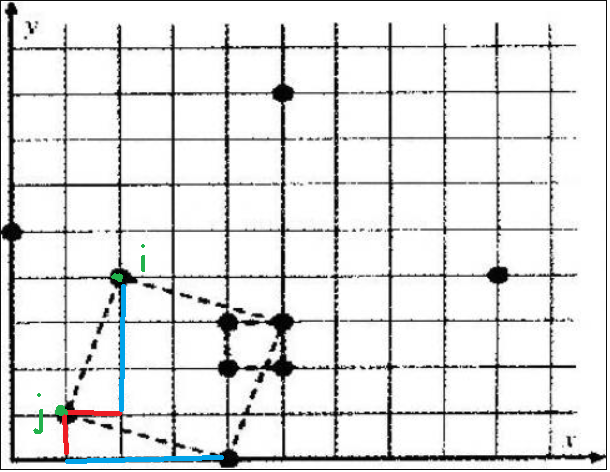
如图所示，我们将左上顶点定为 $i$，左下顶点对应 $j$，那么可以发现如下关系：

1. 标红段为 $i$ 与 $j$ 的横坐标差，正好为左下顶点与右下顶点的纵坐标之差。
2. 标蓝段为 $i$ 与 $j$ 的纵坐标差，正好为左下顶点与右下顶点的横坐标之差。

如此，我们即可仅仅通过两个点推出其余两个点的坐标。

如何求面积

前置知识：勾股定理 $a^2+b^2=c^2$。

把连接 $i$ 和 $j$ 的虚线以及红蓝两线当做一个直角三角形，我们把蓝线想成 $a$，红线想成 $b$，那么虚线长度即正方形的边长，即为 $\sqrt{a^2+b^2}$。再根据正方形面积公式，正方形面积为 $\sqrt{a^2+b^2}\times \sqrt{a^2+b^2}=a^2+b^2$。

完整代码

#include<bits/stdc++.h>
#define max(a,b) a>b?a:b
using namespace std;
bool f[5020][5020];
int x[3020];
int y[3020];
int n,m;
int main()
{
//  freopen("ruin.in","r",stdin);
//  freopen("ruin.out","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",x+i,y+i);
        f[x[i]][y[i]]=1;
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {

            int a=x[i]-x[j];
            int b=y[i]-y[j];
            int Ax=x[i]-b;
            int Bx=x[j]-b;
            int Ay=y[i]+a;
            int By=y[j]+a;  
            if(Ax<1||Ax>5000||Bx<1||Bx>5000||Ay<1||Ay>5000||By<1||By>5000)continue;
            if(f[Ax][Ay]&&f[Bx][By])
            {
                ans=max(ans,a*a+b*b);
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}